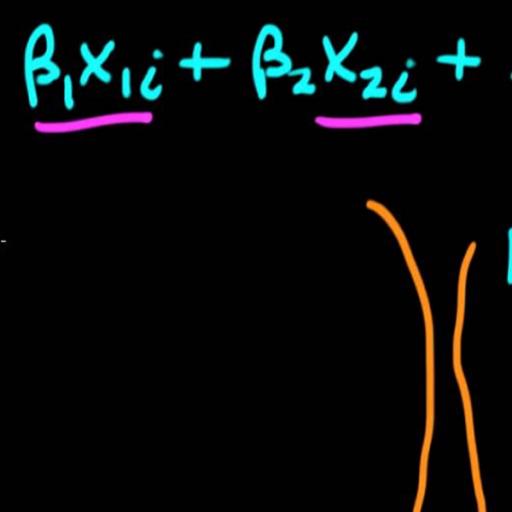Many time-series encountered in practice exhibit characteristics that cannot be appropriately described by linear Gaussian models. For example, a Gaussian linear process {Zt} is time reversible, i.e., the distribution of {Zt1,...,ZtN} is the same as that of {ZtN,...,Zt1}. Deviations from this property are suggested by time-series where the number of ascending periods (i.e., periods with increasing observations) is systematically different from the number of descending periods. In this type of situations, it is often necessary to relax the linear assumption, i.e., it is necessary to consider nonlinear models for the analysis of a time-series. Consequently, it is clear that, before modelling any time-series, it may be necessary to test it for linearity.
This letter presents a method to detect nonlinear dependencies in time series. It is a bicorrelation nonparametric test based on a Box-Cox transformation. Using Monte Carlo results we compare the properties of the suggested test with other four well known tests for such cases. These tests are the The Hinich Portmanteau Bicorrelation Test(1996), McLeodi -Li Test(1983), Test for nonadditivity Keenan (1985), ARCH Test(1982) and the Luukkonen LST 1988 Test. According to our simulation results the suggested test is superior to the other tests in small and large samples.