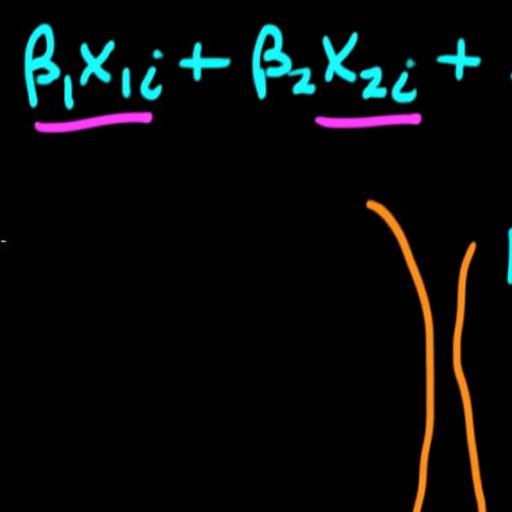This paper addresses the question, how temporal aggregation affects structural inference and special linear and nonlinear Granger causality tests. Indeed this is an important issue, since in practice the frequency of observation is usually different from what may be called the ‘natural’ frequency of the underlying time series. For example, at financial markets, agents react very rapidly to news and, thus, the natural frequency of a model that describes the behavior of financial agents is likely to be minutes rather the hours or days. However, if the natural frequency of the underlying process is high relative to the observed frequency of the data, temporal aggregation and systematic sampling may completely change the structural relations in the system. It is therefore interesting to investigate the effects of temporal aggregation on structural inference and special in the case on nonlinear Granger causality.
Temporal aggregation poses many interesting questions which have been explored in time series analysis and which yet remain to be explored. An early example of research in this area is Quenouille (1957), where the temporal aggregation of ARIMA processes is studied. Amemiya and Wu (1972), and Brewer (1973) review and generalize Quenouille's result by including exogenous variables. Zellner and Montmarquette (1971) discuss the effects of temporal aggregation on estimation and testing. Engle (1969) and Wei (1978) analyze the effects of temporal aggregation on parameter estimation in a distributed lag model. Granger (1987) discusses the implications of aggregation on systems with common factors. Other contributions1 in this area include Tiao (1972), Stram and Wei (1986), Weiss (1984), Granger and Lee (1999), and Marcellino (1999), to name but a few.