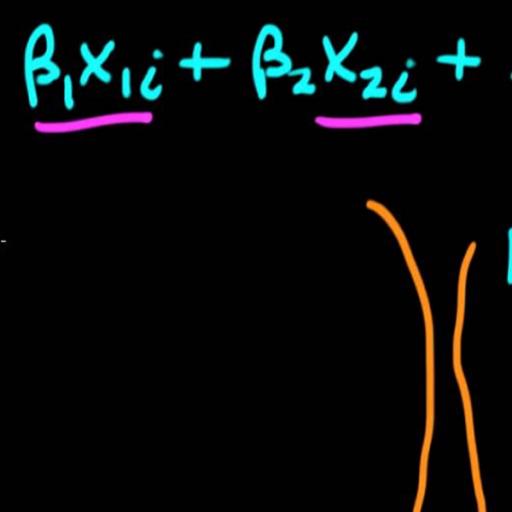Mortality forecast is very important for the governments and the private insurance companies. Government agencies use the results of these forecasts when planning and developing health policy. Insurance companies, also use these predictions to plan their policies and their strategy for retirement systems. The issue of mortality risk and, in particular, of longevity risk has been largely caused the interest of scientific community in recent years, when facing the main problem of pricing the insurance products. This risk, is known in the scientific literature as Longevity Risk, and is the risk derived from a future mortality rate. (Brouhns, et all 2002). The price of any insurance product on the duration of life is based on two types of assumptions - demographical and financial. The assumptions are the main reason for which is necessary to include a forecast of the future trends of mortality.
Thus, it is very important to provide improved mortality forecasts. Moreover, it is a well-known fact that the human mortality globally declined. Improvements in standards of living, sanitary conditions and medicine led to rapidly decreasing mortality rates in the early part of the century. People from all over the world, live more and the costs of the public or private insurance become bigger. Various methods have been developed to improve mortality forecasts. A very popular method of mortality forecasting was introduced by Lee and Carter (1992) to model and forecast U.S. mortality. The main statistical tool of Lee and Carter is the least-squares estimation via singular value decom- position of the matrix of the log age-specific observed forces of mortality together with Box–Jenkins modelling for time series. The method was de- signed for long-term forecasting based on a lengthy time series of historic data. However, significant structural changes have occurred in mortality patterns over our century, reducing the validity of experience in the more distant past for present forecasts.
The future trend of mortality is modelling as a stochastic process. Furthermore, there is always a systematic danger, which is very difficult to eliminate and it is independent from the plenty of policies that an insurance organisation can apply (Denuit and Frostig, 2005). Specifically, Lee-Carter model describes the logarithmically transformed age-specific central rate of death as a sum of:
- the age-specific component that is independent of time
- the product of a time-varying parameter, also known as the mortality index, that summarizes the general level of mortality and an additional age-specific component that represents how rapidly or slowly mortality
- at each age varies when the mortality index changes.
As it is easily understandable, the model is very simple to be applied be- cause it has a limited number of parameters. The Lee Charter model became so popular that it was called “leading statistical model of mortality fore- casting in the demographic literature” (Deaton and Paxson, 2004). However, there were some criticisms for the model. For example, Bell (1997) noted that the model did not fit the jump off data very well. In addition, it was appeared a number of variants, which tried to optimize the initial model of Lee and Charter.