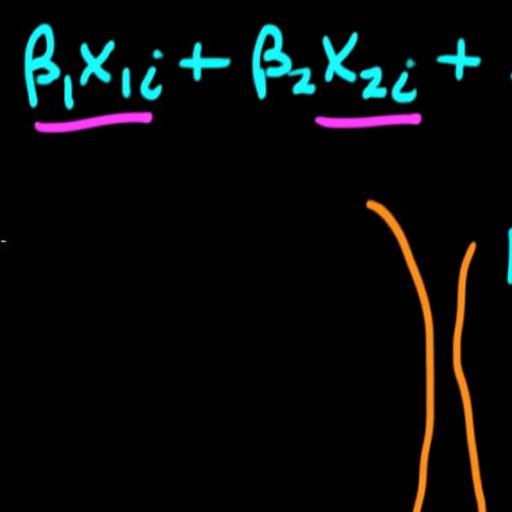The use of panel data has been increasingly popular in empirical microeconomic and macroeconomic studies. An important advantage of using panel data is that researchers can obtain consistent or unbiased estimates of important parameters controlling for unobservable cross-sectional heterogeneity. An example of such heterogeneity, the so-called individual effect, is the effect of talent in a model of workers’ hourly earnings. In order to estimate the effect of education on hourly wage rate consistently, researchers need to control for the heterogeneity in workers’ talents or skills. Unfortunately, data containing information on individual workers’ talents and skills are extremely rare. Without such information, it is extremely difficult, if not impossible, to control for talent using pure cross-sectional data. In contrast, when panel data are available, a variety of estimation methods (e.g., Hausman and Taylor, 1981; Amemiya and MaCurdy, 1986; Cornwell and Rupert, 1988) can be used to control for the unobservable individual effects. Even if individual workers’ talents are unobservable, it is possible to estimate the effect of education on hourly wage consistently.
In this paper we consider a more general panel data model in which the individual effect has multiple components and each of these components is time-varying. Specifically, the model assumes that the unobservable individual effects have a factor structure. For this model, we develop appropriate estimation and model-specification methods. Bai (2005) has considered the same panel factor model that we study in this paper (see also Bai and Ng, 2002; and Bai, 2003). His approach is designed for the analysis of panel data with large numbers of both time series and cross-section observations, and the regressors are assumed to be strictly exogenous to the random error terms in the model. Kneip, Sickles and Song (2005) also consider the same model but with the additional assumption that the factors change slowly and smoothly over time. Our paper is different from these papers in two respects. First, we focus on the case of panel data with a small number of time series observations and a large number of cross-section units (big N and small T). Second, we also consider the case in which some regressors are only weakly exogenous.
Standard panel data models assume that the unobservable individual effect is a single time-invariant component. However, this assumption may be excessively restrictive in practice. For example, consider a model of hourly wage rates. It is a well-known fact that labor productivity changes over the business cycle. Accordingly, the productivity of an individual’s unobservable talent or skill would also change over the business cycle (Ahn, Lee and Schmidt, 2001). If so, the effect of unobservable talent on hourly wages would vary over time because workers’ hourly wage rates depend on their labor productivity. It is also likely that hourly wage rates depend on multiple individual effects. For example, individual workers’ wages would be affected by unexpected changes in macroeconomic variables due to changes in monetary or fiscal policies. However, the effects of these aggregate variables on wages would depend on individual-specific characteristics such as the worker’s residential area and occupation. The panel data models that assume a single time-invariant individual effect are inappropriate for the analysis of data with such multiple time-varying individual effects.
There are many other examples of models that may require multiple time-varying effects. One example is the consumption model based on the life-cycle and rational-expectation hypothesis. This model predicts that current consumption growth depends on the unobservable marginal utility of expected life-time wealth. When consumers’ future incomes are uncertain, their marginal utility of wealth varies over time (Altug and Miller, 1990; Pischke, 1995). Another example is the asset pricing models that assume time-varying risk premia (Campbell, 1987; Ferson and Foerester, 1994; Zhou, 1994). These models can be also viewed as panel data models with unobservable multiple time-varying individual effects. Finally, our approach can be used for the empirical studies of economic growth based on international data (e.g., Mankiw, Romer and Weil, 1992; Islam, 1995; Caselli, Esquival and Lefort, 1996). Individual countries’ economic growth rates could depend on world-wide supply shocks such as the oil shocks in the 1970’s, and the technology shocks we have witnessed from the rapid development of the information technology industry in the 1990’s. However, the effect of such world-wide shocks could depend on country-specific factors such as available human capital and natural resources.
The model we consider is also related to the issue of cross-sectional dependence, which is a growing research area. Many studies based on cross section data assume that the data are cross-sectionally independent. However, there are many cases in which the independence assumption is questionable. As we have discussed above, the decisions of individual economic agents (such as individuals, households, or firms) can depend on common macroeconomic shocks. When data contain such common factors, conventional estimators such as ordinary least squares (OLS) and instrumental-variables can be biased (Andrews, 2003). Even in the cases where such estimators are consistent, the estimated standard errors of the estimators obtained ignoring cross-sectional dependence could be seriously biased (for example, Chang, 2002). In response to these problems, many alternative estimation methods have been developed (Conley, 1999; Kelejian and Prucha, 1999; Chang, 2002). The method we develop in this paper provides an alternative solution for the analysis of panel data. Our model can allow cross-sectional dependence among individual effects.
Panel data models with time-varying individual effects and small numbers of time-series observations have been studied by Holtz-Eakin, Newey and Rosen (1988), Lee (1991), Chamberlain (1992), and Ahn, Lee and Schmidt (2001) [hereafter, ALS]. However, these studies, except Lee (1991), only consider cases with a single individual effect. Lee (1991) considered the case of multiple factors, but he made the unnecessarily strong assumption that the errors are i.i.d. normal, and he assumed that the true number of factors was known.
The goals of this paper are two-fold. The first is to investigate estimation methods that can produce consistent estimates under quite general assumptions. We accomplish this via GMM as opposed to nonlinear least squares. The second is to develop an estimation and testing procedure for the correct number of factors.