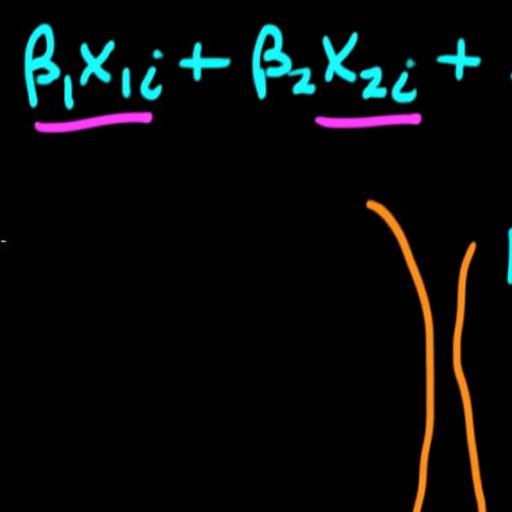This paper is concerned with the construction of confidence intervals for efficiency levels of individual firms in stochastic frontier models with panel data. A number of different techniques have been proposed in the literature to address this problem. Given a distributional assumption for technical inefficiency, maximum likelihood estimation was proposed by Pitt and Lee (1981). Battese and Coelli (1988) showed how to construct point estimates of technical efficiency for each firm, and Horrace and Schmidt (1996) showed how to construct confidence intervals for these efficiency levels. Without a distributional assumption for technical efficiency, Schmidt and Sickles (1984) proposed fixed effects estimation, and the point estimation problem for efficiency levels was discussed by Schmidt and Sickles (1984) and Park and Simar (1994). Simar (1992) and Hall, H ̈ardle, and Simar (1993) suggested using bootstrapping to conduct inference on the efficiency levels. Horrace and Schmidt (1996, 2000) constructed confidence intervals using the theory of multiple comparisons with the best, and Kim and Schmidt (1999) suggested a univariate version of comparisons with the best. Bayesian methods have been suggested by Koop, Osiewalski, and Steel (1997) and Osiewalski and Steel (1998).
In this paper we will focus on bootstrapping and some related procedures. We provide a survey of various versions of the bootstrap for construction of confidence intervals for efficiency levels. We also propose a simple alternative to the bootstrap that uses standard parametric methods, acting as if the identity of the best firm is known with certainty. We present Monte Carlo simulation evidence on the accuracy of the bootstrap and our simple alternative. Finally, we present some empirical results to indicate how these methods work in practice.